Sub-Riemannian manifold
In mathematics, a sub-Riemannian manifold is a certain type of generalization of a Riemannian manifold. Roughly speaking, to measure distances in a sub-Riemannian manifold, you are allowed to go only along curves tangent to so-called horizontal subspaces.
Sub-Riemannian manifolds (and so, a fortiori, Riemannian manifolds) carry a natural intrinsic metric called the metric of Carnot–Carathéodory. The Hausdorff dimension of such metric spaces is always an integer and larger than its topological dimension (unless it is actually a Riemannian manifold).
Sub-Riemannian manifolds often occur in the study of constrained systems in classical mechanics, such as the motion of vehicles on a surface, the motion of robot arms, and the orbital dynamics of satellites. Geometric quantities such as the Berry phase may be understood in the language of sub-Riemannian geometry. The Heisenberg group, important to quantum mechanics, carries a natural sub-Riemannian structure.
Contents |
Definitions
By a distribution on  we mean a subbundle of the tangent bundle of
we mean a subbundle of the tangent bundle of  .
.
Given a distribution 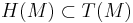 a vector field in
a vector field in 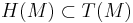 is called horizontal. A curve
is called horizontal. A curve  on
on  is called horizontal if
is called horizontal if 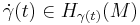 for any
for any  .
.
A distribution on 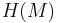 is called completely non-integrable if for any
is called completely non-integrable if for any 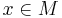 we have that any tangent vector can be presented as a linear combination of vectors of the following types
we have that any tangent vector can be presented as a linear combination of vectors of the following types ,\ [A,[B,C]](x),\ [A,[B,[C,D]]](x),\dots\in T_x(M)](/2012-wikipedia_en_all_nopic_01_2012/I/155a3cbcde20a47d7185c9fabc6a104c.png) where all vector fields
where all vector fields 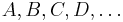 are horizontal.
are horizontal.
A sub-Riemannian manifold is a triple 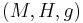 , where
, where  is a differentiable manifold,
is a differentiable manifold,  is a completely non-integrable "horizontal" distribution and
is a completely non-integrable "horizontal" distribution and  is a smooth section of positive-definite quadratic forms on
is a smooth section of positive-definite quadratic forms on  .
.
Any sub-Riemannian manifold carries the natural intrinsic metric, called the metric of Carnot–Carathéodory, defined as
where infimum is taken along all horizontal curves ![\gamma: [0, 1] \to M](/2012-wikipedia_en_all_nopic_01_2012/I/9f4bf5bc55f62b0bbe89e8775d5fd2e2.png) such that
such that 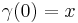 ,
, 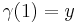 .
.
Examples
A position of a car on the plane is determined by three parameters: two coordinates  and
and  for the location and an angle
for the location and an angle  which describes the orientation of the car. Therefore, the position of car can be described by a point in a manifold
which describes the orientation of the car. Therefore, the position of car can be described by a point in a manifold
One can ask, what is the minimal distance one should drive to get from one position to another? This defines a Carnot–Carathéodory metric on the manifold
A closely related example of a sub-Riemannian metric can be constructed on a Heisenberg group: Take two elements  and
and  in the corresponding Lie algebra such that
in the corresponding Lie algebra such that
spans the entire algebra. The horizontal distribution  spanned by left shifts of
spanned by left shifts of  and
and  is completely non-integrable. Then choosing any smooth positive quadratic form on
is completely non-integrable. Then choosing any smooth positive quadratic form on  gives a sub-Riemannian metric on the group.
gives a sub-Riemannian metric on the group.
Properties
For every sub-Riemannian manifold, there exists a Hamiltonian, called the sub-Riemannian Hamiltonian, constructed out of the metric for the manifold. Conversely, every such quadratic Hamiltonian induces a sub-Riemannian manifold. The existence of geodesics of the corresponding Hamilton–Jacobi equations for the sub-Riemannian Hamiltonian are given by the Chow–Rashevskii theorem.
References
- Bellaïche, André; Risler, Jean-Jacques, eds. (1996), Sub-Riemannian geometry, Progress in Mathematics, 144, Birkhäuser Verlag, ISBN 978-3-7643-5476-3, MR1421821, http://books.google.com/books?id=7Z7IMze7pDwC
- Gromov, Mikhael (1996), "Carnot-Carathéodory spaces seen from within", in Bellaïche, André; Risler., Jean-Jacques, Sub-Riemannian geometry, Progr. Math., 144, Basel, Boston, Berlin: Birkhäuser, pp. 79–323, ISBN 3-7643-5476-3, MR1421823, http://www.ihes.fr/~gromov/PDF/carnot_caratheodory.pdf
- Le Donne, Enrico, Lecture notes on sub-Riemannian geometry, http://www.math.ethz.ch/~ledonnee/sub-Riem_notes.pdf
- Richard Montgomery, A Tour of Subriemannian Geometries, Their Geodesics and Applications (Mathematical Surveys and Monographs, Volume 91), (2002) American Mathematical Society, ISBN 0-8218-1391-9.
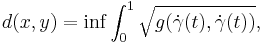
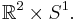
![\{ \alpha,\beta,[\alpha,\beta]\}](/2012-wikipedia_en_all_nopic_01_2012/I/3192b3f083a241d7d2c87f29bc56b634.png)